(draft)梯度下降算法

RAWCODE

• Keys
  • Newton Method
• Defination
• Draft
• Gradient descent
  • BGD (batch gradient descent)
  • SGD (stochastic gradient descent)
  • MGD (mini-batch gradient descent)
• Algorithms
  • Momentum
  • NAG (Nesterov's accelerated gradient)
  • Adagrad
  • Adadelta
    • Accumulate Over Window
    • Correct Units with Hessian Approximation
  • RMSprop
  • Adam
  • AdaMax
  • Nadam
  • AMSGrad
• Compare
• References

1 Keys

损坏函数(误差函数), 凸误差函数, 非凸误差函数, 学习率, 鞍点, 参数更新, 海瑟矩阵, 指数衰减, 泰勒级数

1.1 Newton Method

牛顿法的基本思想是利用迭代点\(x_k\)处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次 模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值.

核心思想是对函数进行泰勒级数展开

2 Defination

w.r.t. : with regard to

Gradient descent is a way to minimize an objective function \(J(\theta)\) parameterized by a model's parameters \(\theta \in \mathbb R^d\) by updating the parameters in the opposite direction of the gradient of the objective function \(\nabla_\theta J(\theta)\) w.r.t. to the parameters. The learning rate \(\eta\) determines the size of the steps we take to reach a (local) minimum.

ruder.ioAn overview of gradient descent optimization algorithms

3 Draft

优化计算目标函数的梯度需要根据使用的数据的量的多少进行在精度和时间上权衡去择取合适的算法.

对于凸误差函数,批梯度下降法能够保证收敛到全局最小值,对于非凸函数,则收敛到一个局部最小值.

4 Gradient descent

代码实现(old)

代码实现(new)

4.1 BGD (batch gradient descent)

批量梯度下降

Defination:

Vanilla gradient descent computes the gradient of the cost function w.r.t. to the parameters \(\theta\) for the entire training dataset: \[ \theta = \theta - \eta \nabla_\theta J(\theta) \]

对全部训练数据进行依次更新, 如果数据集比较大, 造成冗余计算.

Code:

for i in range(nb_epochs):
    params_grad = evaluate_gradient(loss_function, data, params)
    params = params - learning_rate * params_grad

4.2 SGD (stochastic gradient descent)

随机梯度下降法, 有时也叫on-linegradient descent, 对每一条训练数据进行一次更新.

Defination:

Stochastic gradient descent (SGD) performs a parameter update for each training example \(x^{(i)}\) and label \(y^{(i)}\): \[ \theta = \theta - \eta \nabla_\theta J(\theta; x^{(i)}; y^{(i)}) \]

对每条训练数据进行一次更新, 更新频繁会出现\(J\)值的上下波动, 反而可能跳到新的,潜在的更好的局部最优 上.

Codes:

for i in range(nb_epochs):
    np.random.shuffle(data)
    for example in data:
        params_grad = evaluate_gradient(loss_function, example, params)
        params = params - learning_rate * params_grad

4.2.1 SGD with Gaussian Noise

Results in Deep Learning never cease to surprise me. One ICLR 2016 paper from Google Brain team suggests a simple 1-line code change to improve your parameter estimation across the board — by adding a Gaussian noise to the computed gradients. Typical SGD updates parameters by taking a step in the direction of the gradient (simplified): \[ \mathbf{\Theta}_{t+1} \leftarrow \mathbf{\Theta}_{t} + \alpha_{t}\nabla\mathbf{\Theta} \] Instead of doing that the suggestion is add a small random noise to the update: \[ \mathbf{\Theta}_{t+1} \leftarrow \mathbf{\Theta}_{t} + \alpha_{t}(\nabla\mathbf{\Theta} + N(0, \sigma_t^2)) \] Further, \(\sigma\) is prescribed to be: \[ \sigma_t^2 = \frac{\eta}{(1 + t)^{0.55}} \] and \(\eta\) is one of \(\{0.01, 0.3, 1.0\}\)!

Deplip RaoMake your Stochastic Gradient Descent more Stochastic

4.3 MGD (mini-batch gradient descent)

小批量梯度下降法

Defination:

Mini-batch gradient descent finally takes the best of both worlds and performs an update for every mini-batch of n training examples: \[ \theta = \theta - \eta \nabla_\theta J(\theta; x^{(i, i+n)}; y^{(i, i+n)}) \]

Codes:

for i in range(nb_epochs):
    np.random.shuffle(data)
    for batch in get_batches(data, batch_size=50):
        params_grad = evaluate_gradient(loss_function, batch, params)
        params = params - learning_rate * params_grad

对一组训练数据进行一次更新, 解决了SGD的跳动带来的收敛不稳定的问题, 有时机器学习中SGD可能就是指的是MGD.

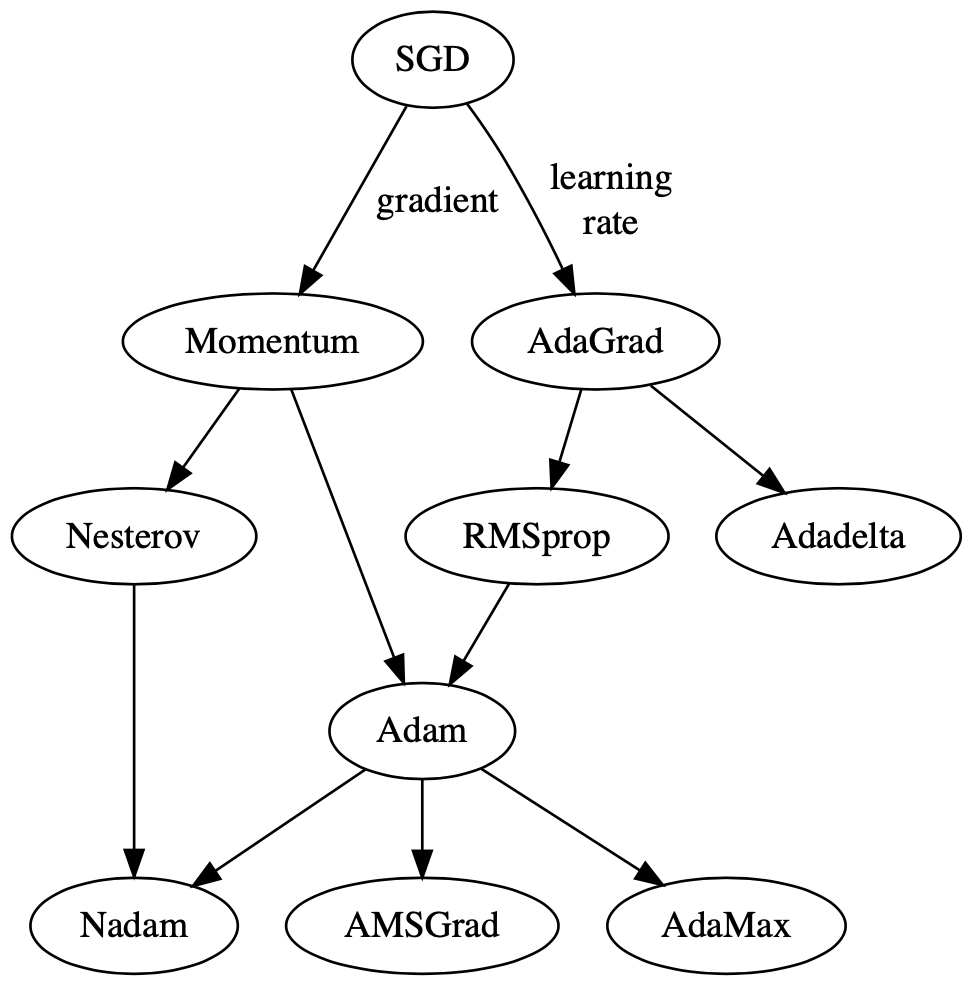
5 Algorithms

上面传统的梯度下降最优算法与将要介绍的下面的算法有些不同, 下面将要介绍的算法learning rate会变化, 传统的算 法则是单一的learning rate进行更新权重.

算法关系

5.1 Momentum

动量法

Defination:

Momentum is a method that helps accelerate SGD in the relevant direction and dampens oscillations. It does this by adding a fraction \(\gamma\) of the update vector of the past time step to the current update vector:

\[ \begin{align} \begin{split} v_t &= \gamma v_{t-1} + \eta \nabla_\theta J( \theta) \\ \theta &= \theta - v_t \end{split} \end{align} \]

SGD波动最容易发生在局部最优处, 假设从山顶到山底通过一个斜坡滑下(最斜的一条), 则动量会累加, 即越靠近山底, 滑下的速度越快, SGD因为抖动做不到, 而动量法的原理就是在从山顶到山底滑下的通道上(梯度向量)加上一个累加 分量\(\gamma\)(衰减因子), 如果滑下的过程中斜坡不变, \(\gamma\)一直累加, 即参数更新的step变大, 收敛更快.

The momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions. As a result, we gain faster convergence and reduced oscillation.

ruder.iomomentum

Codes:

for i in range(nb_epochs):
    np.random.shuffle(data)
    for batch in get_batches(data, batch_size=50):
        params_grad = evaluate_gradient(loss_function, batch, params)
        v[:] = momentum * v + learning_rate * params_grad
        params = params - v

5.2 NAG (Nesterov's accelerated gradient)

内斯特罗夫加速梯度(Look ahead)

动量法的高阶版本

Defination:

Nesterov accelerated gradient (NAG) is a way to give our momentum term this kind of prescience, so we look ahead by calculating the gradient not w.r.t. to our current parameters \(\theta\) but w.r.t. the approximate future position of our parameters: \[ \begin{align} \begin{split} v_t &= \gamma v_{t-1} + \eta \nabla_\theta J( \theta - \gamma v_{t-1} ) \\ \theta &= \theta - v_t \end{split} \end{align} \]

理解NAG, 关键要理解超前预知, 比如, 沿着斜坡下滑, 根据当前的下滑加速度(momentum), 提前预知下一时刻会到 达何处, 如果下一时刻到达的地方的斜率和当前不一样(eg.相反), 及时调整了加速度.

收敛速度比动量更新方法更快,收敛曲线更加稳定.

Momentum vs NAG:

图片来自¹

5.3 Adagrad

适应性梯度算法, 梯度二阶矩

Defination:

Adagrad adapts the learning rate to the parameters, performing smaller updates (i.e. low learning rates) for parameters associated with frequently occurring features, and larger updates (i.e. high learning rates) for parameters associated with infrequent features.

单个参数更新形式1: \[ \begin{align*} g_{t, i} &= \nabla_\theta J( \theta_{t, i} ) \\ \theta_{t+1, i} &= \theta_{t, i} - \eta \cdot g_{t, i} \\ \theta_{t+1, i} &= \theta_{t, i} - \dfrac{\eta}{\sqrt{G_{t, ii} + \epsilon}} \cdot g_{t, i} \\ \end{align*} \]

\(G_{t} \in \mathbb{R}^{d \times d}\) is a diagonal matrix.

矩阵向量更新形式2: \[ \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{G_{t} + \epsilon}} \odot g_{t} \]

这个算法存在一个问题, \(G_{t}\)记载所有参数历史梯度累加平方和, 在整个训练过程中, 这个累加和不断增大, 这会导 致学习率变小, 无限变小时, 这个算法就会再也获取不到额外的信息.

\(G_{t}\)可以表示为:\(\sum_{\tau=1}^{t}(g_{\tau})^{2}\), 注意累加的是梯度(gradient),不是参数\(\theta\).

由\(\Delta \theta_{t} = - \dfrac{\eta}{\sqrt{\sum_{\tau=1}^{t}(g_{\tau})^{2} + \epsilon}} \odot g_{t}\)得:

• 训练前期激励阶段: 累加梯度平方值小, 从而\(\Delta \theta_{t}\)值较大, 参数变化明显.

• 训练后期惩罚阶段: 累加梯度平方值大, 从而\(\Delta \theta_{t}\)值较小, 参数变化非常小 (缺点).

5.4 Adadelta

自适应学习率调整, 梯度二阶矩均值

Defination:

Adadelta is an extension of Adagrad, Instead of accumulating all past squared gradients, Adadelta restricts the window of accumulated past gradients to some fixed size \(w\)

正如上面描述的Adagrad的缺点, 如果数据集很大, 会导致累加的梯度平方和很大, 导致继续训练很难得到额外的信 息. Adadelta试图寻找一个平衡, 不用计算所有的(时间序列)梯度平方和, Adagrad为了每次计算所有的梯度平方和, 需要额外保存历史梯度值的记录, Adadelta是将梯度的平方和递归的表示成所有历史梯度平方的衰减均值: the sum of gradients is recursively defined as a decaying average of all past squared gradients.

注意, 因为即使存放\(w\)个之前的梯度(对窗口w中的梯度求和), 这方法也是低效的, 所以最终采用的对所有梯度平方衰减 均值的方式实现.

TODO

不明白什么是decaying average?, 为了继续下面的内容, 对decaying average的理解, 可以先用下面的例 子忽悠一下 (纯属自娱自乐):

hypothesis data: \(x_1, x_2, \cdots, x_n\)

then: \(E[x]_n = \dfrac{1}{n}\sum_{i}^{n} x_i \label{adadelta_1} \tag{1}\)

if we insert \(x_{n+1}\) into data: \(x_1, x_2, \cdots, x_n, x_{n+1}\)

then: \(E[x]_{n+1} = \dfrac{1}{n+1} \sum_{i}^{n+1} x_i \label{adadelta_2} \tag{2}\)

from (\(\ref{adadelta_1}\)) and (\(\ref{adadelta_2}\)) we can get:

\[ \begin{align*} E[x]_{n+1} &= \dfrac{nE[x]_n + x_{n+1}}{n+1} \\ &= \dfrac{n}{n+1}E[x]_n + \dfrac{1}{n+1} x_{n+1} \end{align*} \]

if let \(\gamma = \dfrac{n}{n+1}\)

then: \(1-\gamma = \dfrac{1}{n+1}\)

then: \(E[x]_{n+1} = \gamma E[x]_n + (1-\gamma)x_{n+1}\)

5.4.1 Accumulate Over Window

已知前面元素的均值, 在训练过程中不断加入新值, 再重新计算所有元素均值, 使用近似的方法(个人认为这也是why call decaying)求得, 忽略真实的训练次数, 使用\(\gamma\)表示: \[ E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g^2_t \]

使用(平方和)均值的方式可以杜绝(解决)Adagrad累加(平方和)渐进增大的问题.

with the decaying average over past squared gradients:

\[ \Delta \theta_t = - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t} = - \dfrac{\eta}{RMS[g]_{t}} g_t \]

最终得到Accumulate Over Window的形式为:

\[ \begin{align*} \theta_{t+1} &= \theta_t + \Delta \theta_t \\ &= \theta_t - \dfrac{\eta}{RMS[g]_{t}} g_t \end{align*} \]

5.4.2 Correct Units with Hessian Approximation

TODO 没明白, 后续补充, 先把公式列出:

\[ E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1 - \gamma) \Delta \theta^2_t \]

\[ RMS[\Delta \theta]_{t} = \sqrt{E[\Delta \theta^2]_t + \epsilon} \]

\[ \begin{align} \begin{split} \Delta \theta_t &= - \dfrac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}} g_{t} \\ \theta_{t+1} &= \theta_t + \Delta \theta_t \end{split} \end{align} \]

5.5 RMSprop

均方根传播, Adadelta的一个特殊情况 (Accumulate Over Window)

RMSprop and Adadelta have both been developed independently around the same time stemming from the need to resolve Adagrad's radically diminishing learning rates.

\[ \begin{align} \begin{split} E[g^2]_t &= 0.9 E[g^2]_{t-1} + 0.1 g^2_t \\ \theta_{t+1} &= \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t} \end{split} \end{align} \]

5.6 Adam

Adaptive Moment Estimation 自适应矩估计 亚当

Adam可以看做是RMSprop和动量法的结合.

一阶矩(均值) with exponentially decaying average of past gradients \(m_t\):

\[m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\] like momentum.

二阶矩(非中心的方差) with exponentially decaying average of past squared gradients \(v_t\):

\[v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2\] like Adadelta or RMSprop.

偏差校正:

\[ \begin{align} \begin{split} \hat{m}_t &= \dfrac{m_t}{1 - \beta^t_1} \\ \hat{v}_t &= \dfrac{v_t}{1 - \beta^t_2} \end{split} \end{align} \]

and last:

\[ \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t \]

算法完美, 既使用到了momentum的动量特性(梯度方向不变, 越来越快), 同时具有RMSprop的自动更新学习速率.

5.7 AdaMax

亚当的变种, L范数

TODO

\[ \begin{align} \begin{split} u_t &= \beta_2^\infty v_{t-1} + (1 - \beta_2^\infty) |g_t|^\infty\\ & = \max(\beta_2 \cdot v_{t-1}, |g_t|) \end{split} \end{align} \]

\(\theta_{t+1} = \theta_{t} - \dfrac{\eta}{u_t} \hat{m}_t\)

5.8 Nadam

Nesterov-accelerated Adaptive Moment Estimation, 那达慕, 带有Nesterov动量项的亚当

Nadam (Nesterov-accelerated Adaptive Moment Estimation) thus combines Adam and NAG. 即它是Adam和NAG的组合

回顾一下Momentum动量formulas:

\[ \begin{align*} g_t &= \nabla_{\theta_t}J(\theta_t)\\ m_t &= \gamma m_{t-1} + \eta g_t\\ \theta_{t+1} &= \theta_t - m_t \end{align*} \]

回顾一下NAG具有预测能力(先一步\(J(\theta_t - \gamma m_{t-1})\))的算法 formulas:

\[ \begin{align*} g_t &= \nabla_{\theta_t}J(\theta_t - \gamma m_{t-1}) \\ m_t &= \gamma m_{t-1} + \eta g_t \\ \theta_{t+1} &= \theta_t - m_t \end{align*} \]

从上面的公式会发现动量计算出现2处, 一处为了更新梯度\(J(\theta_t - \gamma m_{t-1})\), 另一处最后更新参数时, Dozat提出了一种方式修正NAG (look-ahead of weights, not gradient):

\[ \begin{align*} g_t &= \nabla_{\theta_t}J(\theta_t) \\ m_t &= \gamma m_{t-1} + \eta g_t \\ \theta_{t+1} &= \theta_t - (\gamma m_t + \eta g_t) \end{align*} \]

回顾一下Adam:

\[ \begin{align*} m_t &= \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ v_t &= \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 \\ \hat{m}_t & = \frac{m_t}{1 - \beta^t_1} \\ \hat{v}_t &= \dfrac{v_t}{1 - \beta^t_2} \\ \theta_{t+1} &= \theta_{t} - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t \\ \theta_{t+1} &= \theta_{t} - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\frac{\beta_1 m_{t-1}}{1 - \beta^t_1} + \dfrac{(1 - \beta_1) g_t}{1 - \beta^t_1}) \end{align*} \]

Nadam真容:

\[ \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\beta_1 \hat{m}_t + \dfrac{(1 - \beta_1) g_t}{1 - \beta^t_1}) \]

把\(\dfrac{m_{t-1}}{1 - \beta_1^t} = \hat{m_{t-1}}\)换成\(\hat{m_t}\) ignore that the denominator is \(1 - \beta^t_1\) and not \(1 - \beta^{t-1}_1\)

5.9 AMSGrad

TODO

6 Compare

算法	优点	缺点	适用情况
BGD	目标函数为凸函数时,可以找到全局最优值	收敛速度慢,需要用到全部数据,内存消耗大	不适用于大数据集,不能在线更新模型
SGD	避免冗余数据的干扰,收敛速度加快,能够在线学习	更新值的方差较大,收敛过程会产生波动,可能落入极小值(卡在鞍点),选择合适的学习率比较困难(需要不断减小学习率)	适用于需要在线更新的模型,适用于大规模训练样本情况
Momentum	能够在相关方向加速SGD,抑制振荡,从而加快收敛	需要人工设定学习率	适用于有可靠的初始化参数
Adagrad	实现学习率的自动更改	仍依赖于人工设置一个全局学习率,学习率设置过大,对梯度的调节太大.中后期,梯度接近于0,使得训练提前结束	需要快速收敛,训练复杂网络时;适合处理稀疏梯度1
Adadelta	不需要预设一个默认学习率,训练初中期,加速效果不错,很快,可以避免参数更新时两边单位不统一的问题	在局部最小值附近震荡,可能不收敛	需要快速收敛,训练复杂网络时
Adam	速度快,对内存需求较小,为不同的参数计算不同的自适应学习率	在局部最小值附近震荡,可能不收敛	需要快速收敛,训练复杂网络时;善于处理稀疏梯度和处理非平稳目标的优点,也适用于大多非凸优化 - 适用于大数据集和高维空间

7 References

• http://ruder.io/optimizing-gradient-descent/
• https://blog.csdn.net/google19890102/article/details/69942970
• https://blog.csdn.net/yzy_1996/article/details/84618536
• http://louistiao.me/notes/visualizing-and-animating-optimization-algorithms-with-matplotlib/
• https://towardsdatascience.com/10-gradient-descent-optimisation-algorithms-86989510b5e9
• https://colab.research.google.com/drive/1Xsv6KtSwG5wD9oErEZerd2DZao8wiC6h
• https://mc.ai/learning-parameters-part-2-momentum-based-and-nesterov-accelerated-gradient-descent/
• https://gist.github.com/akshaychandra21
• https://blog.csdn.net/yzy_1996/article/details/84618536
• https://www.cnblogs.com/neopenx/p/4768388.html

---

1. https://mc.ai/learning-parameters-part-2-momentum-based-and-nesterov-accelerated-gradient-descent↩